Wie in dem anderen Beitrag gezeigt, erfolgt die Umwandlung von einem Koordinatensystem in ein anderes fast durchweg mit Hilfe von Matrix-Multiplikationen. Nur die lokalen Koordinaten eines Meshs gehen als Vektoren in die Multiplikationskette ein. Das Bild zeigt die Kette, und zwar so, wie sie rechnerisch gehandhabt wird. Die Faktoren sind nicht vertauschbar, und es wird grundsätzlich von links nach rechts gerechnet, vom Globalen zum Lokalen, also entgegengesetzt der Darstellung im oben verlinkten Beitrag. aber auch entgegengesetzt der üblichen Denk- bzw. Vorstellungsrichtung. Matrizen werden häufig mit Großbuchstaben dargestellt.

P = Projektionsmatrix
V = Viewmatrix
M = Modelmatrix

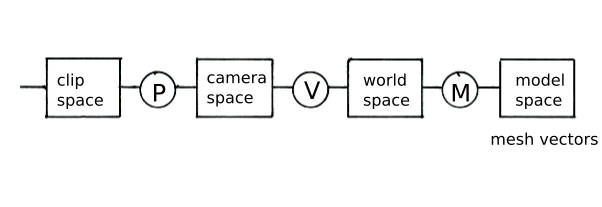
Eine vollständige Berechnungskette sieht demnach so aus:

Hierbei ist zu beachten, dass die Modelmatrix wiederum das Produkt von maximal 5 Matrizen sein kann (je eine für die Postionierung und Skalierung, drei für die Rotationen um die 3 Achsen). Ähnliches gilt für die Viewmatrix, wenngleich hierbei die Skalierung entfällt und die Rotation auch direkter mit Hilfe von Quaternionen erfolgen kann. Doch für die Gesamtübersicht ist das eher nicht von Bedeutung, auch die Reihenfolge dieser Matrixmultiplikationen zweiter Ordnung folgt eigenen Regeln.

Mit Ausnahme der finalen Multiplikation mit den Meshvektoren können die Matrixoperationen wahlweise auf der Grafikkarte, also im Shader, erfolgen oder im Anwendungsprogramm im CPU-Raum. Was günstiger ist, hängt u.a. davon ab, welche Zwischenwerte an welchen Stellen erforderlich sind. Die Multiplikationskette kann nämlich unterbrochen werden, wobei die Richtung links - rechts immer beizubehalten ist. Oft wird z.B. außerhalb des Shaders eine Modelview-Matrix erstellt

und an den Shader übergeben. Dort kann die MV-Matrix für beliebige Berechnungszwecke verwendet werden, etwa für die Berechnung der Beleuchtungssituation, wozu dann zusätzlich die Vertexnormalen herangezogen werden. Die endgültige Vertexposition ergibt sich dann so:

Oder folgende Situation: In einer Szenerie befinden sich sehr viele Objekte, z.B. Bäume. Alle Objekte werden innerhalb eines Frames im selben Viewspace gezeichnet; folglich braucht die Multiplikation PV = P * V nur einmal pro Frame stattzufinden. Der Rest PV * M * mesh_vector wird denn für jedes Objekt durchgeführt. In einer Landschaft mit 500 oder 1000 Bäumen kann sich das durchaus günstig auf die Performance auswirken.